The Topology of Polyhedra, Coffee Mugs, and Neurons
- Tejasi Bhatnagar
- Feb 6, 2021
- 9 min read
Updated: Feb 6, 2021
The study of shapes, angles, and lines came naturally to us. The Egyptians in 3,000 BC. built the pyramids, surveyed the land and mapped the stars in the night sky. All of these, along with a multitude of activities required us to measure, design, and build diverse forms and structures. Fast forward the timeline to the Greeks, they referred to this study as geometry (measuring the earth). They studied the properties of circles, ellipses and parabolas deriving motivation from astronomy and optics. They gave us the Pythagoras theorem, approximated pi and above all, organized geometry as we see it today. Bulk of this organization was done in Euclid’s elements which proposed that pretty much anything in geometry can be proved step by step if we systematically build on five truths or axioms.
In this article, we wish to talk about a relatively younger branch of geometry called topology. In contrast to classical geometry, that dealt with measurements and calculations of rigid shapes, topology studies objects up to shrinking, stretching, and molding. For example, a triangle is topologically the same as a circle since we can smoothen its edges to make it round. In fact, topology does not distinguish between any polygon. We say that two objects are topologically the same if one can be continuously transformed into the other. Cutting or tearing is not allowed. Here is an animation to justify the famous saying “A topologist cannot distinguish between a coffee mug and a doughnut.”

Source: https://www.youtube.com/watch?v=dwrhCSORERA and gifs.com
The birth of topology: Euler’s seven bridge problem and the Euler characteristic.
This story goes back to the 18th century, set in the town of Königsberg in Prussia. Königsberg was a beautiful city located on the banks of the river Pregel. It was one of the most prominent cities of Prussia in terms of economic and cultural growth, and as we will see, also mathematically relevant.

The city of Königsberg back in the day.
The river divided the city into four different landmasses connecting each other with seven bridges. As folklore goes, the people of the town while taking walks on weekends came up with a game: Is there a way to roam around the city while traveling each bridge only once? They tried many different paths but could not find one that would win the game. The news soon reached Leonard Euler (pronounced “oiler”), a mathematician at heart who contributed to many, many fields like mechanics, astronomy, optics, and hydraulics.
The question may seem trivial at first. However, as Euler himself wrote in a letter to his friend: “It seemed worthy of attention as it required in that (neither) geometry, nor algebra, nor even the art of counting could solve it.” Well, one way to think about this problem is to sit down with a map of Königsberg and trace down different paths along the seven bridges. Given enough mental energy, we could eliminate many of them which travel any bridge more than once. However, how do we know that we have exhausted all the possible paths? In today’s world, we could determine all of them easily with the help of a computer program, but Euler’s simple reasoning was a stepping stone to what can now be translated into the language of graph theory, a field that would revolutionize computation theory and give us the Web.
So, how did Euler solve the problem? He suggested that instead of looking at the entire town, let’s focus on the bridges and shrink the regions between them to thick dots (nodes). Euler’s map looked something like this:

Euler’s argument is elegant: While traversing each bridge, we first enter a node and then leave it. If each bridge is traveled only once, each node should have an even number of bridges through them, except the nodes where we start and end our journey. If we look closely at the above graph, each node has an odd number of bridges going out and coming in. Thus, such a path is not possible.
Besides the graph we saw, Euler’s insight concerned the geometry of the problem at hand. He noticed that the problem did not use the standard methods of geometry known at the time, rather it required understanding the “geometry of position”. This seemingly effortless idea led to the imagination of topology.
Another milestone worth mentioning is the Euler characteristic formula. One of the fundamental objects of study in ancient times was the polyhedra. The Greeks admired them deeply. They believed that beauty of the universe is found in symmetry and perfection, proposing that the five regular polyhedra form the building blocks of all matter and even constitute the solar system. However, early studies of these shapes were all based on the properties that could be measured such as the angles, length of the sides and area of the faces. Euler’s remarkable formula gave a combinatorial relationship between the number of vertices (V), faces (F) and edges (E) of a polyhedron. He discovered that for any polyhedron: V+F-E = 2. For example, the tetrahedron shown below has 4 vertices, 4 faces, and 6 edges, thus satisfying the formula. This seemed so elementary that even Euler wondered how the Renaissance mathematicians missed this. Because of the restrictions imposed on the vertices, edges, and faces by the equation, the formula helps us classify all the types of regular polyhedra that can exist. There are only five such!

Source: https://mathshistory.st-andrews.ac.uk/Diagrams/PlatonicSolids.html
Above all, this formula encodes the information of how 3-D polyhedra are built from low dimensional objects like straight lines and triangles. This simple idea laid the foundation of one of the many important characteristics of surfaces we study today.
How do we think about surfaces?
After Euler’s ideas, the study of surfaces considerably developed the field of topology. In contrast to the Greeks, Bernhard Riemann, a German mathematician, was studying surfaces in higher dimensions. His ideas would later help develop Einstein’s general theory of relativity, providing the mathematical framework for the theory of space-time curvature. Anyway, Riemann was interested in classifying different kinds of surfaces which led him to the study of “holes”. For example, a (hollow) sphere has no holes. On the other hand, the doughnut has one hole. We call this surface a torus.
Much of topology came into picture building on Riemann’s simple question: When are two surfaces the “same”? Imagine for a second that we have a hollow clay ball. If you make a hole in your ball, we get something like this. Flatten it a little bit and you get a plane!
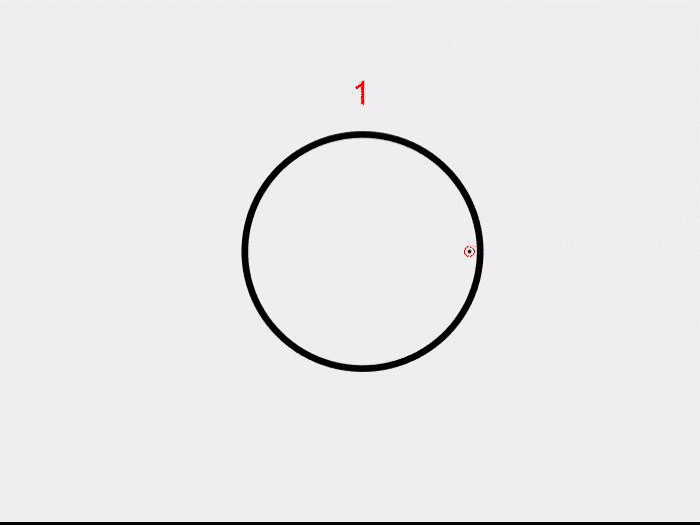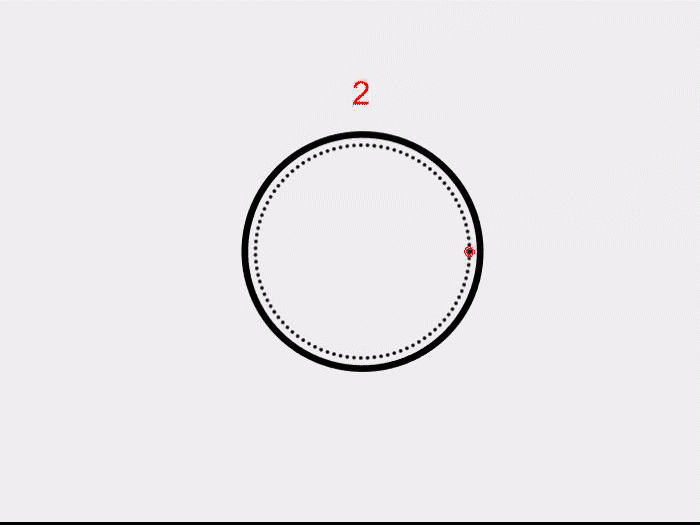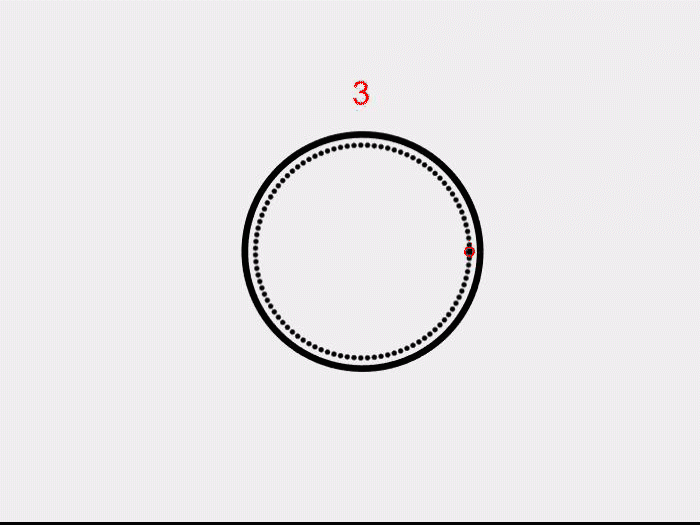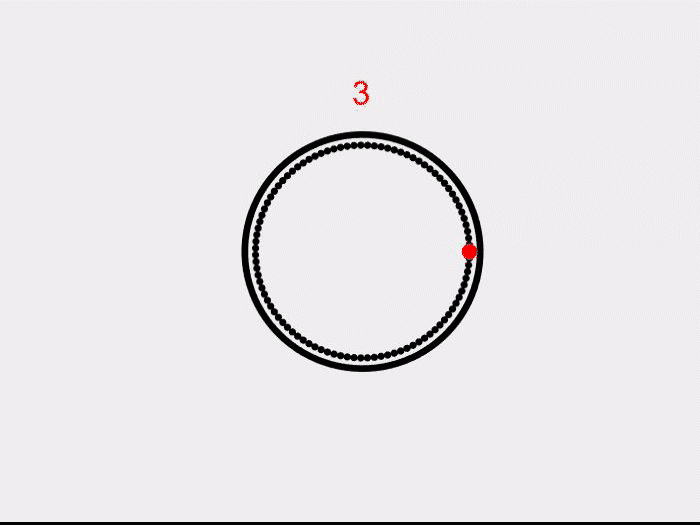
Now let’s make one more hole in the plane. If we shrink the region, around the hole as shown, we get a circle. In the universe of topology, we say that a sphere with a hole is the same as a plane, while a plane with a hole is just a circle.

Now, can we stretch and shrink the ball to make it into a torus? Maybe not! At some point, we would need to remove and reattach some parts of the clay to make a hole. This is where the Euler characteristic, in all its true glory, will solve our problem. Notice that a sphere is topologically the same as a tetrahedron. We can compute its Euler characteristic by the above formula to get 2. Similarly, to compute for the torus, we triangulate the doughnut as shown below. Using the formula, we get 0. The characteristic is an algebraic invariant of surfaces. If two surfaces are topologically the same, they will have the same number, no matter how we “triangulate” it. Since the torus and the sphere have different characteristics, they are topologically different.

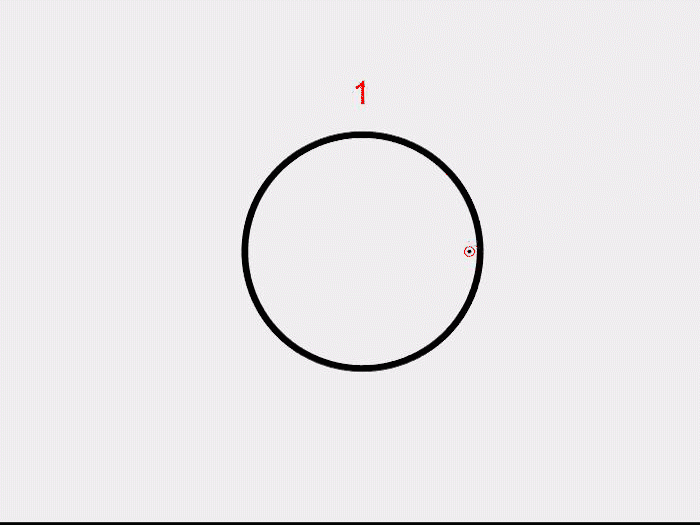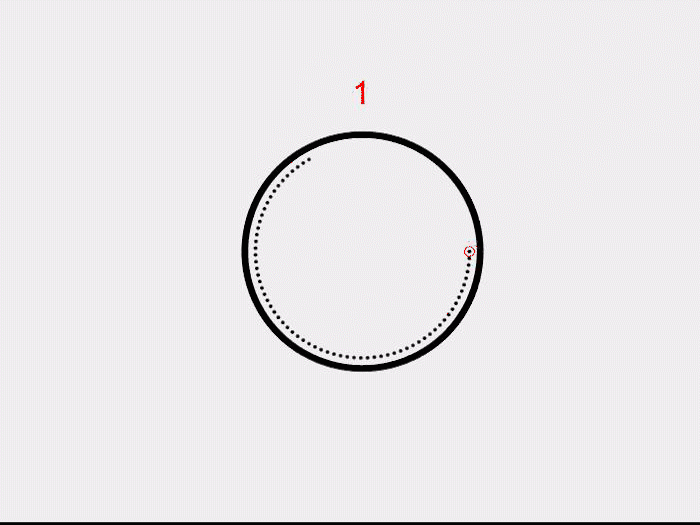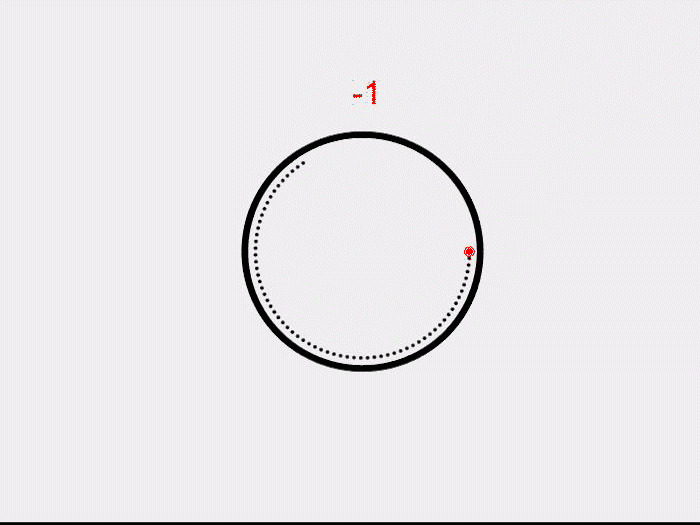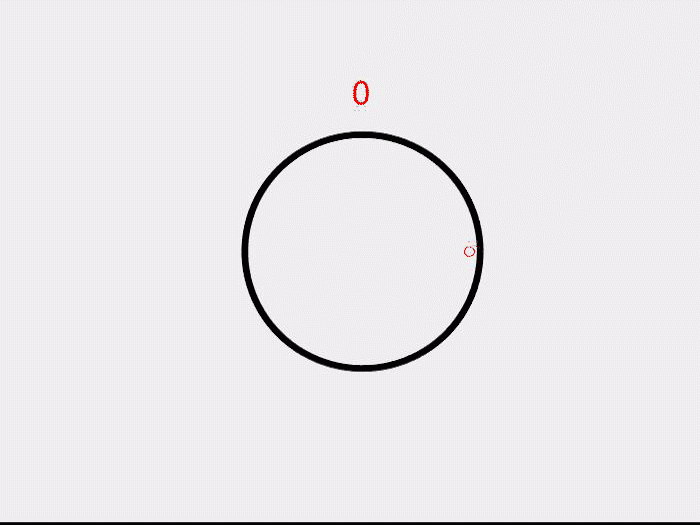
In 1895, Poincare in his seminal paper Analysis situs, associated certain algebraic structures to surfaces, transforming how we think about geometry. His idea was to look at all the “loops” on a surface. These surprisingly form an algebraic structure. For a very simple example, let us look at a circle. What are the possible “loops” that we can draw on a circle? Well, we could go clockwise once, twice or thrice and so on. We could also go anti-clockwise several times. But how do we get an algebraic structure? Associate the integer 1 to the loop that goes clockwise once, 2 to going around twice and so on. Similarly, -1 to the loop that goes anti-clockwise once, following the same pattern to other negative integers. Now, just as we add the integers, we can add ‘’loops’’ on a circle as well. Going clockwise once and then twice is the same as going clockwise three times. This coincides with the addition of the corresponding numbers! Similarly going clockwise once and then anti-clockwise, “shrinks” the two paths and we are left with the point at which we started. A point on a circle can also be thought of as a trivial loop and is assigned the integer 0.
This way, we associate the integers to the circle.
Let’s look at one more example to make this a little clearer. The following video shows a loop on a sphere that eventually shrinks to a point on top. In fact, all the loops we draw can be shrunk this way to a point. We call such loops “trivial”. Thus, we associate only 0 to the sphere corresponding to all the trivial loops.

Credits for the sphere and circle animation: Nitin Burman
Poincare wondered if we could determine surfaces using these algebraic invariants. In some sense yes: If two surfaces are topologically the same, then they will have the same invariant. Since the circle and the sphere have different algebraic structures associated to them, they cannot be continuously transformed into each other. A fact intuitively clear. But the other way round is not true. All the loops on the plane and the sphere can be shrunk to a point, but they are not the same. In addition to the baby examples we saw, the theory of algebraic topology develops a wide range of tools to help us study geometrical objects in arbitrary dimensions.
Now, it is said that Poincare did not really carry out all the algebra behind his constructions. A lot of it was done by Emmy Noether, a brilliant mathematician who contributed immensely to the field of abstract algebra revolutionizing many neighboring fields such as modern physics and geometry. She introduced what are known as homology groups, a class of algebraic invariants that give a much cleaner theory as we see it today.
The topology of neurons: computational methods
One of the most fascinating topics I came across while writing this article was that of using tools in topology to understand big data sets. Turns out that topological analysis of data (TDA) is being used to gain insights on a wide variety of themes such as cancer genomics, swarm behavior of birds and insects, and understanding the human brain. As the scientists working in this field aptly say, “the data has shape and the shape matters.”
The fundamental idea behind such methods is to develop tools that give us characteristics of the collective data set. Analogous to the stretching and shrinking of objects before, any small perturbations to the set should not change the information we get. Consider the data points below. We aim to systematically organize it by associating a geometrical complex to it. For instance, let us draw balls of radius 1 cm about each data point. We join two points with a line if they lie on two overlapping circles and we join three or more points with a triangle if they lie in more than two overlapping circles. As you might already have noticed, we get a figure with a hole in between. Now, instead of looking at one fixed radius, we vary the distance and see how the “hole” in the data set changes. Initially we get many gaps if the radius is too small for the circles to overlap, but as the distance becomes bigger, the central hole emerges, ultimately vanishing when the circles are too big, and everything overlaps.

Converting this in the language of barcodes, we have something like this.

The small bar encodes the initial “gaps” which we don’t really care about, while the long bar code gives us the essential information about the hole in the data. The method we use to extract algebraic information by associating family of geometric simplices to our data is known as persistence homology.
In 2005, the Blue Brain Project was founded by the Brain and Mind Institute of EPFL in Switzerland. The initiative aims to build biologically detailed reconstructions and simulations of the mouse brain. Among their many projects, one studies complex branching patterns in neurons using computational topology. The method is similar. We identify a largest component of the neuron cell, for example the long red nerve shown in the figure. We then compute the radial distance from its root node (R) to the points as we move along the small branches. This data is then converted to barcodes and diagrams which interpret distances as points in the coordinate plane.

Source: https://link.springer.com/article/10.1007%2Fs12021-017-9341-1
The figure below shows comparison in neuronal morphologies of various animal species like cat (I), dragonfly (II), fruit-fly (III), mouse (IV), and rat (V). The encoded barcode assigns a unique topological signature to the neurons, thus providing a mechanism to quantify diverse neuronal branching structures.

source: https://link.springer.com/article/10.1007%2Fs12021-017-9341-1
Warning: If you did get interested in whatever I told you, so much so that you decide to take a course on algebraic topology, let me warn you that you will not really encounter any of the stuff I said in such primitive form, rather it will be enveloped in mathematical rigor. What you might see on the blackboard will be something like:

But I assure you that at the heart of all the serious mathematics they do, topologists are just finding ways to drink their coffee from doughnuts!
References
This article was inspired by many videos and blogs I found while prepping for it.
(For math grads and undergrads) Pierre Albin’s lectures in topology on YouTube are super nice. They helped me build a lot of intuition in the subject and pass my quals. Its first lecture gives an overview of the history of topology and the timeline we follow is mainly inspired by it.
Articles from Britannica helped me get the story right in many contexts.
Some other related material: MAA’s article on the seven-bridge problem, Britannica's article on the same.
The last section on computational methods is inspired by Mathew Wright’s wonderful video. I just put his video into words. Also, Gunnat Carlsson’s talk on “Topological modelling of complex data” at JMM 2018 is very nice.
Here is the Blue Brain Project’s website. This is the paper I referred to and the pictures at the end are from here, too!






Comments